Linear Algebra

1.How to check if the point is in a rotated bbox?

1.1 get the vertices of the rotated bbox *

dims = bbox[3:6]
locs = bbox[0:3]
rots = bbox[6]    
kitti_rots = -rots - np.pi / 2


#class_name = l.split(' ')[0]
#dims = np.array(l.split(' ')[8:11], dtype=np.float64)
#locs = np.array(l.split(' ')[11:14], dtype=np.float64)
#rots = np.array(l.split(' ')[14:15], dtype=np.float64)
#dims = dims[[2, 0, 1]]

## transfer the rotation angle to kitti format
##kitti_rots = -rots[0] - np.pi / 2
## transer the dims and locs into kitti format
##locs = locs[[2, 0, 1]]
##locs[2] -= dims[1] / 2
##locs[1] -= dims[0] / 2


# generate 8 vertices from the bounding box's dims locs and rotation
vertices = np.array([
    [-dims[0] / 2, -dims[1] / 2, -dims[2] / 2],
    [dims[0] / 2, -dims[1] / 2, -dims[2] / 2],
    [dims[0] / 2, dims[1] / 2, -dims[2] / 2],
    [-dims[0] / 2, dims[1] / 2, -dims[2] / 2],
    [-dims[0] / 2, -dims[1] / 2, dims[2] / 2],
    [dims[0] / 2, -dims[1] / 2, dims[2] / 2],
    [dims[0] / 2, dims[1] / 2, dims[2] / 2],
    [-dims[0] / 2, dims[1] / 2, dims[2] / 2],
], dtype=np.float64)
# rotate the vertices
rotMat = np.array([
    [np.cos(rots), -np.sin(rots), 0],
    [np.sin(rots), np.cos(rots), 0],
    [0, 0, 1]
], dtype=np.float64)
vertices = np.dot(vertices, rotMat)
# translate the vertices
vertices = vertices + locs

1.2 check if point is in the b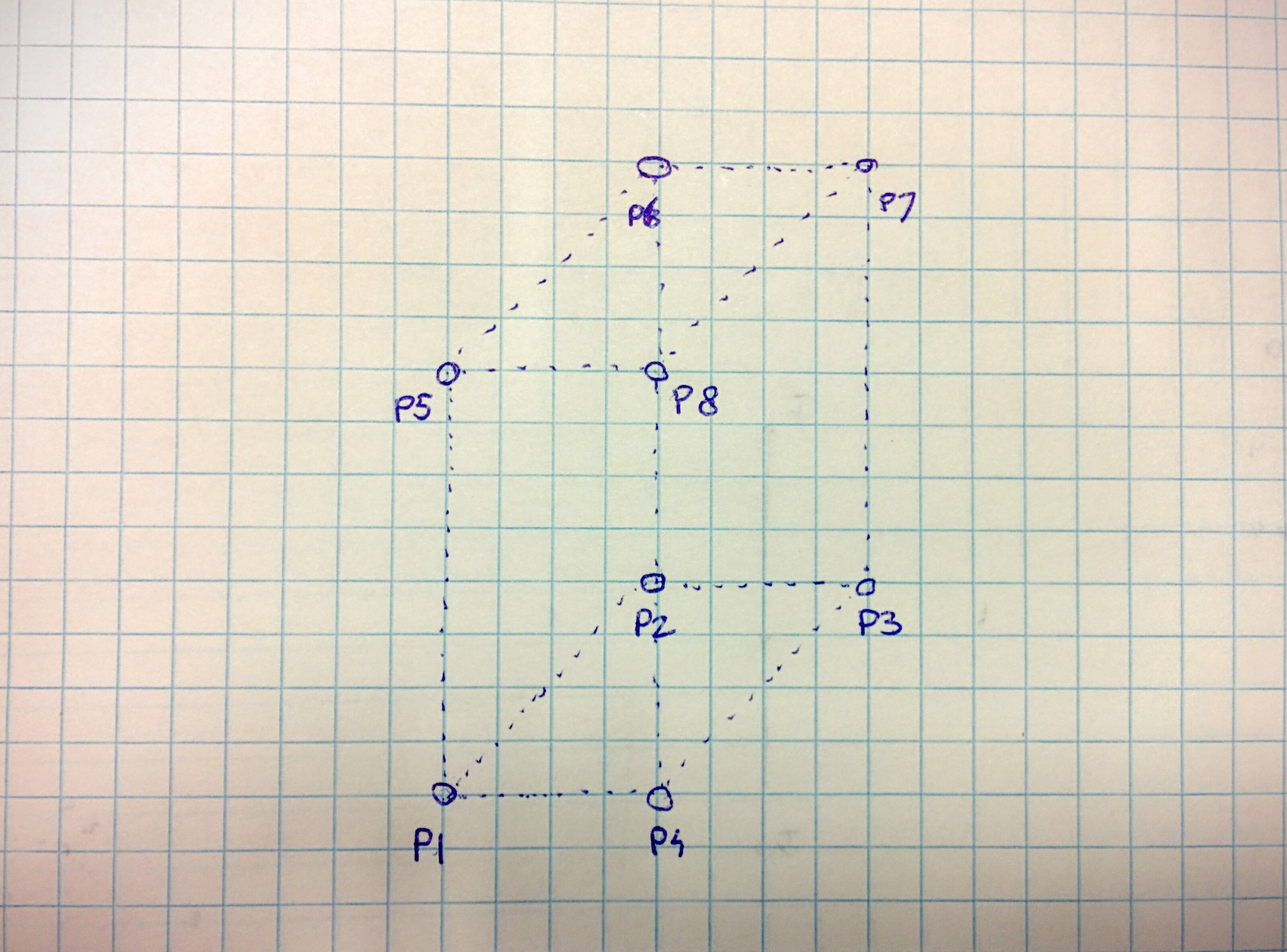box * the vertices seems like the above image The three important directions are u=P1−P2, v=P1−P4 and w=P1−P5. They are three perpendicular edges of the rectangular box.

A point x lies within the box when the three following constraints are respected:

The dot product $u \cdot x$ is between $u \cdot P_1$ and $u \cdot P_2$

The dot product $v \cdot x$ is between $v \cdot P_1$ and $v \cdot P_4$

The dot product $ w \cdot x$ is between $w \cdot P_1$ and $w \cdot P_5$

EDIT: If the edges are not perpendicular, you need vectors that are perpendicular to the faces of the box. Using the cross-product, you can obtain them easily:

$$ u=(P1−P4)×(P1−P5) $$

$$ v=(P1−P2)×(P1−P5) $$

$$ w=(P1−P2)×(P1−P4) $$

then check the dot-products as before.

def find_pts_in_box3d(pts, vertices):
    a01 = vertices[1] - vertices[0]
    a03 = vertices[3] - vertices[0]
    a04 = vertices[4] - vertices[0]
    dot010 = np.dot(a01, vertices[0])
    dot011 = np.dot(a01, vertices[1])
    dot030 = np.dot(a03, vertices[0])
    dot033 = np.dot(a03, vertices[3])
    dot040 = np.dot(a04, vertices[0])
    dot044 = np.dot(a04, vertices[4])
    indices = []
    for ind, pt in enumerate(pts):
        if np.dot(a01, pt) >= dot010 and np.dot(a01, pt) <= dot011 and \
           np.dot(a03, pt) >= dot030 and np.dot(a03, pt) <= dot033 and \
           np.dot(a04, pt) >= dot040 and np.dot(a04, pt) <= dot044:
            indices.append(ind)
    return indices